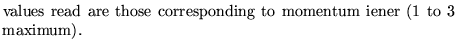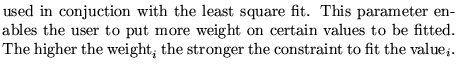Next: Baseline definition
Up: Operations used in conjunction
Previous: Operations used in conjunction
This operations allows the user to fit the values read in monitors (see their
definition in the machine list). Any parameter can be used as
variable. Successive use of this operation can simulate progressive
alignment correction of a beamline. A new minimizer is installed
since December 1 1984. It has a default tolerance and default
increments for the variables which seem adequate. As a consequence the
input parameters del(i) have no influence. We have kept them to avoid
changes in the input format .
Input format
ALIGnment fitting .....(maximum 80 characters)
nstep nit nvar ncond nfit nopter
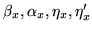
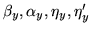
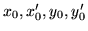
dx dx' dy dy'
nener 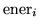 for i from 1 to nener
for i from 1 to nener
Origin
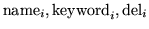 for i from 1 to npar
for i from 1 to npar
When nfit equals 1 or 2 the following group applies
CORR
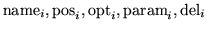 for i from 1 to ncor
for i from 1 to ncor
NOTE: ncor+npar=nval
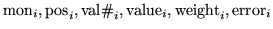 for i from 1 to ncond
for i from 1 to ncond
End of the group for nfit 1 or 2
If nfit equals 3 the following group applies :
CORR
mcorr
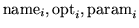 for i from 1 to mcorr
for i from 1 to mcorr
nmon nskip
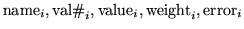 ) for i from 1 to nmon
) for i from 1 to nmon
end of group for nfit 3
nasp
repeat the following nasp times
name keywd npas
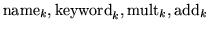 for k from 1 to npas
for k from 1 to npas
Parameter definitions
nstep 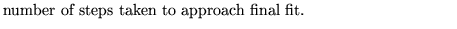
nit 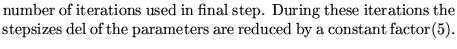
nvar 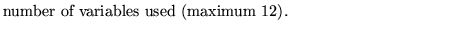
ncond 
nfit 
1 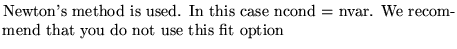
2 
nopter 
0 
1 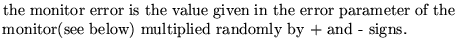
2 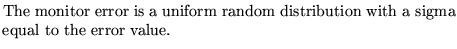
3 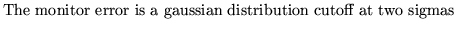
4 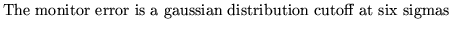
11,12,13,14 
The initial seed used is the same as that defined by the operation
SEED. The generation of the random errors for the monitors is,
INDEPENDENT of that of the misalignments and of the field errors.
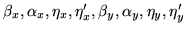
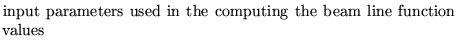
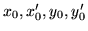

dx dx' dy dy' 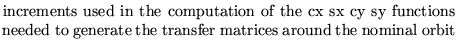
nener 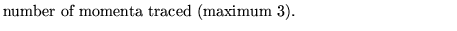
ener 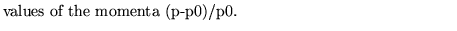
origin 
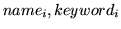
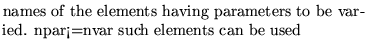
del 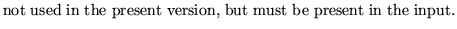
CORR 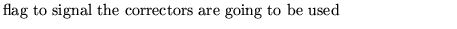
mcor 


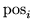

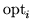
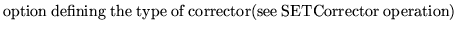
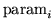
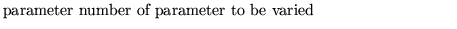

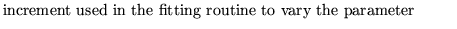
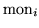
nmon 
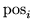
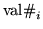

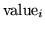
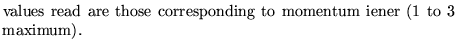

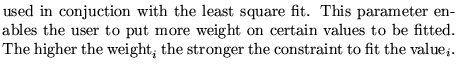


nasp: 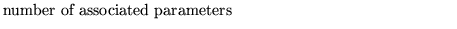
name1 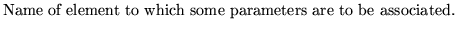
keywd 
npas 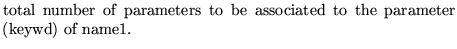
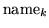
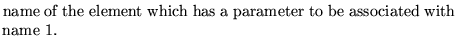
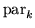
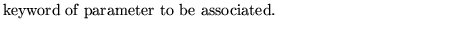
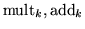

Examples
The first two examples are taken from demo6.
The third set comes from demo7. Please refer to these demos for
their relation with other operations.
* the following is an example of an Alignment fitting with nfit = 3
ALIGNMENT FITTING
0 1 8 8 3 0
3 0 0 0 1 0 0 0
0 0 0 0
0.00001 0.00001 0.00001 0.00001
1 0
MRKC2
CORR
2
HC 0 4
kcv 3 2
2 0
PMC 1 0.0 1.0 20E-06
PMC 2 0.0 1.0 20E-06
0,
* the following is an example of an Alignment fitting with nfit = 2
ALIGNMENT FITTING
0 1 6 6 2 0
3 0 0 0 1 0 0 0
0 0 0 0
0.00001 0.00001 0.00001 0.00001
1 0
MRKS1
corr
ksv 2 3 2 0.0001 ksv 16 3 2 0.0001 ksv 35 3 2 0.0001
ksh 7 3 1 0.0001 ksh 19 3 1 0.0001 ksh 32 3 1 0.0001
PMs 13 1 0.0 1.0 20E-06 PMs 13 2 0.0 1.0 20E-06
PMs 28 1 0.0 1.0 20E-06 PMs 28 2 0.0 1.0 20E-06
PMs 40 1 0.0 1.0 20E-06 PMs 40 2 0.0 1.0 20E-06
0,
* the following is an example of an Alignment fitting with nfit = 2
* and shows how to correct off momentum orbits and beam sigma
* values
ALIGNMENT CORRECTION FINAL FOCUS ORBIT
0 1 6 6 2 0
49.26950355 0 0 0 22.75617615 0 0 0
0 0 0 0
0.000001 0.000001 0.000001 0.000001
2 0 -0.001
MFIN
KORS DXP 0.000001 KORS DYP 0.000001
KETA DXP 0.000001 KETA DYP 0.000001
KORT DXP 0.000001 KORT DYP 0.000001
PMINT 28 1 0.0 1.0 10E-06 PMINT 28 2 0.0 1.0 10E-06
PMINT 31 5 0.0 1.0 10E-06 PMINT 31 6 0.0 1.0 10E-06
PMINT 33 1 0.0 1.0 10E-06 PMINT 33 2 0.0 1.0 10E-06
0,
ALIGNMENT CORRECTION FINAL FOCUS SIGMAS
0 2 4 6 2 0
49.26950355 0 0 0 22.75617615 0 0 0
0 0 0 0
0.000001 0.000001 0.000001 0.000001
3 0 -0.003 0.003
MFIN
QC1 K1 0.0001 QS1 K1 0.0001
Q3XC K1 0.0001 Q2BA K1 0.0001
PMINT 31 3 1.2E-06 1.0 0.000 PMINT 31 4 1.2E-06 1.0 0.000
PMINT 31 7 1.2E-06 1.0 0.000 PMINT 31 8 1.2E-06 1.0 0.000
PMINT 31 11 1.2E-06 1.0 0.000 PMINT 31 12 1.2E-06 1.0 0.000
0,



Next: Baseline definition
Up: Operations used in conjunction
Previous: Operations used in conjunction
Dobrin Kaltchev
2004-10-20