next up previous
Next: Matrix computation Up: Use and description of Previous: Line geometric aberrations :one

Machine and beam parameters computations

Computes $\beta,\ \alpha, \ \eta, \ \eta ', \ \nu$ values at selected points around the machine. If requested beam parameters are computed. In some cases, the optimum coupling values may be meaningless(if coupling is > 1). 

Input Format 


MACHine and beam parameters....(up to 80 char) 


e1 e2 de nlum dnu nint nbunch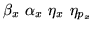 

$ \beta_{x} \ \alpha_{x} \ \eta_{x} \ \eta_{p_{x}} $ 

$ \beta_{y} \ \alpha_{y} \ \eta_{y} \ \eta_{p_{y}} $ mprint [list]

Note: if e1 is zero then nlum is assumed 0 and the input twiss parameters values are those obtained in a previous matrix analysis. If e1 is non zero but $\beta_{x} $ is zero, the first line of parameters must be given and the initial twiss parameters values will be those of the preceding matrix analysis. Parameter definitions

e1 start momentum for beam data and luminosity computations.

e2 end momentum

de momentum step

nlum

0 $\textstyle \parbox{10cm}{no beam size related computations are done.}$

1 $\textstyle \parbox{10cm}{ synchrotron integrals and basic beam size computations are done.}$

2 $\textstyle \parbox{10cm}{ Full luminosity computations are made.}$

dnu dnu value used for optimum luminosity computation.

nint number of interaction regions

nbunch number of bunches

$\beta_{x}...\eta_{p_{y}}$

function values at starting point of lattice.

mprint

-2 $\textstyle \parbox{10cm}{ no printing of results}$

-1 $\textstyle \parbox{10cm}{ print final result only.}$

0 $\textstyle \parbox{10cm}{ print all intermediary and final results.}$

n $\textstyle \parbox{10cm}{ ${\rm n}>0$\ is used with list. There are n intervals in which printing will occur.}$

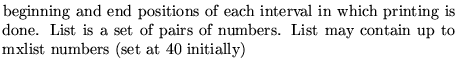
list $\textstyle \parbox{10cm}{ beginning and end positions of each interval in whi... ...airs of numbers. List may contain up to mxlist numbers (set at 40 initially)}$



Examples

The first example, from demo2, shows a general use of this operation.

The second example from demo9 shows how to use this operation when one needs only the list of the twiss parameters around the lattice. Notice that in this case the operation must be preceded by a matrix analysis and that both motions (horizontal and vertical) must be stable. 

MACHINE AND BEAM PARAMETERS. NO LUMINOSITY COMPUTATIONS.
1 1.2 .2 0 0.025 1 1
21.357376 0 0 0 3.940971 0 0 0 1 1 53,

MACH
0,

next up previous
Next: Matrix computation Up: Use and description of Previous: Line geometric aberrations :one
Dobrin Kaltchev 2004-10-20