Layout printing of machine

Computes the geometry of the lattice

Input format 


LAYOut printing of machine..(up to 80 char) 


s x y z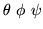 $\theta \ \phi \ \psi$ 


conv mprint [list]

Parameter definitions

s x y z $\theta \ \phi \ \psi$

$\parbox{10cm}{ coordinates of starting point in some absolute refe... ... roll) around the z axis (positive when the x axis turns towards the y axis)}$

conv

$\parbox{10cm}{ conversion factor to enable the printout in various ... ... microns. However, any conversion factor is accepted even if not recognized.}$

mprint

-2 $\parbox{10cm}{ no printing of results.}$

-1 $\parbox{10cm}{ printing final result only.}$

0 $\parbox{10cm}{ print all intermediate and final results.}$

n $\parbox{10cm}{ n$>0$\ used with list, there are n intervals in which printing will occur.}$

list

$\parbox{10cm}{ contains the beginning and the end of all intervals ... ...airs of numbers. List may contain up to mxlist numbers (set at 40 initially)}$

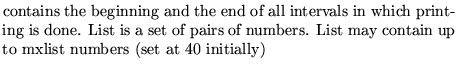
Examples

The example taken from demo1 will give the coordinates of the endpoint of the lattice and the angles defined by the tangent to the reference trajectory within an absolute reference system. The units used are meters.

layout
0 0 0 0 0 0 0 1.0 -1,